O problema: determinar o menor conjunto convexo que contém um determinado conjunto finito de pontos.
Fecho Convexo Bidimensional (FC2D): dado um conjunto C = {p1, p2, ..., pn} de pontos do plano, obter o fecho convexo de C.
A resolução de FC2D requer ordenar n vetores 2D, o que é pelo menos tão complexo quanto ordenar n números reais. Para tal, nos trabalhos realizados de fecho convexo, os vetores são ordenados utilizando pseudo-ângulo em quadrado unitário.
Determinar o fecho convexo de um conjunto de n pontos do plano requer, na verdade, no pior caso, Ω(n log n) passos.
Algoritmos:
1. "Força bruta"
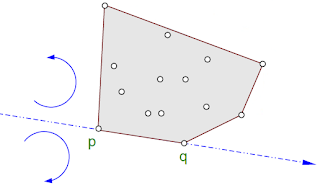
Seja (p, q) todos os pares de pontos pertencentes ao conjunto C. Qualquer par que tenha todos os demais pontos de um único lado em relação à aresta, trata-se de uma aresta válida para o fecho convexo.
3. Graham
4. Dividir-para-conquistar:
4.1. Quickhull (em analogia com Quicksort)
4.2. Mergehull (em analogia com Mergesort)
Os algoritmos de Jarvis e Graham serão melhor explorados nas futuras postagens.

Nenhum comentário:
Postar um comentário