Fecho Convexo 2D: Algoritmo de Graham

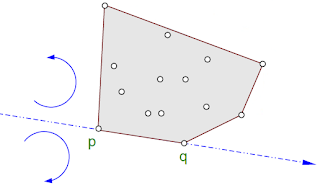
A ideia chave no algoritmo de Graham é a seguinte: a determinação dos pontos extremos pode ser feita de modo eficiente se os pontos p1, p2, ..., pn tiverem sido previamente ordenados polarmente em torno de um ponto interior ao seu fecho convexo. No caso da minha implementação, foi utilizada pseudo-ângulo em quadrado unitário para realizar essa ordenação polar.

O polígono p1, ..., pn possui a propriedade de que existe um ponto interno (o) que vê cada vértice do polígono. Desta forma, a etapa de ordenação reduz o problema de encontrar o fecho convexo de {p1, p2, ..., pn} ao problema de encontrar o fecho convexo de um polígono estrelado. O problema se resume em determinar quais do pontos de C são efetivamente vértices do fecho.

Tendo o polígono estrelado P = p1p2...pn, determinamos o fecho convexo testando se o ângulo interno em cada pi é convexo. Em caso afirmativo, o polígono estrelado é convexo. Caso contrário, removemos de P o ponto pi que viola a condição de convexidade e repetimos o teste para o novo polígono estrelado. O processo continua até que todos os pontos restantes determinem ângulo convexos.

Entretanto, o algoritmo implementado tem algumas alterações: ele não volta à estaca zero cada vez que um ponto pi é retirado do conjunto C.

1. Determina-se o vértice de maior abscissa (suponha que seja p1).

2. O algoritmo examina sucessivamente os vértices p2, p3, ..., até encontrar um pi para o qual o ângulo interno correspondente não seja convexo. Neste ponto, ao invés de recomeçar todo o processo, observamos que a remoção de pi afeta apenas o teste de convexidade do vértice imediatamente anterior.

3. Se o ângulo pi-2pi-1pi+1 continuar sendo convexo, o algoritmo pode continuar, examinando o ângulo em pi+1. Se o ângulo em pi-1 for côncavo, pi-1 é eliminado e o ângulo em seu predecessor reavaliado.

Pseudo-código

Algoritmo de Graham

   pn+1 = p1  //feche o ciclo

   q1 = p1      //p1 é um ponto do fecho convexo

   q2 = p2      //inclua p2 tentativamente

   h = 2

   para i = 3..n+1

      enquanto h > 1 e o ângulo entre qh-1, qh e pi não for convexo

         h = h - 1  //remova qh

      h = h + 1

      qh = pi       //inclua pi tentativamente

Ao final, q conterá os h vértices do fecho convexo.

Desta forma, o algoritmo consiste em ordenar polarmente os pontos de C (O(log n)) e aplicar o algoritmo de Graham (O(n)). Portanto, obtemos o fecho convexo em tempo O(n log n). O algoritmo, portanto, é ótimo para FC2D.

Interface do programa que implementa o algoritmo de Graham:

Demonstração:

Obtenha o código aqui (arquivo protegido por senha): https://dl.dropboxusercontent.com/u/21447748/ConvexHull.rar

Fecho Convexo 2D: Algoritmo de Jarvis

1. Obter um dos vértices do conjunto de pontos. No meu algoritmo, tomo o ponto de menor ordenada (suponhamos que tal ponto seja p1). Se houver mais de um ponto com a mesma ordenada mínima, tomamos entre eles o de maior abscissa.

2. O ponto que se segue a p1 no fecho convexo no sentido anti-horário pode ser obtido da seguinte forma: tomamos a semi-reta paralela ao semi-eixo horizontal positivo Ox passando por p1 e giramos tal semi-reta em torno de p1 no sentido anti-horário até que um ponto p2 seja atingido. Caso mais de um ponto se encontrar sobre sobre a semi-reta, tomamos o ponto mais distante de p1).

3. A partir de p2, giramos a semi-reta obtida prolongando p1p2 também no sentido anti-horário, até determinar p3, e assim por diante, até que retornemos ao ponto p1.

Pseudo-código:

Algoritmo de Jarvis

   p1 = ponto de ordenada mínima

   p2 = próximo(p1, (1,0))

   i = 2

   repita

      pi+1 = próximo(pi, pipi-1)

      i = i+1

   até que pi = p1

Esse algoritmo determina corretamente o fecho convexo, mas não é ótimo. A determinação do vértice seguinte requer tempo O(n). Como é possível que cada ponto de C seja vértice, esta determinação ocorre também O(n) vezes, resultando em um algoritmo O(n²).

Portanto, para melhorar o desempenho, o método que adotei foi o seguinte:

   1. Geração de n pontos aleatoriamente.

   2. Classificação por pseudo-ângulos.

Ao pegarmos o ponto de menor y, calculamos, para todos os outros pontos, os seus valores de pseudo-ângulo.

Depois, selecionamos o de menor valor e usamos ele como base para o cálculo dos outros valores de pseudo-ângulo. O algoritmo continua até que o ponto encontrado na n-ésima iteração, ou seja, no primeiro ponto.

Cálculo dos pseudo-ângulos a partir do ponto inicial (marcado com 0)

 Acompanhe nos slides abaixo o funcionamento do algoritmo que implementei:

Código disponível para download exclusivo do professor da disciplina: https://dl.dropboxusercontent.com/u/21447748/ConvexHull.rar

Fecho Convexo

O problema: determinar o menor conjunto convexo que contém um determinado conjunto finito de pontos.

Fecho Convexo Bidimensional (FC2D): dado um conjunto C = {p1, p2, ..., pn} de pontos do plano, obter o fecho convexo de C.

A resolução de FC2D requer ordenar n vetores 2D, o que é pelo menos tão complexo quanto ordenar n números reais. Para tal, nos trabalhos realizados de fecho convexo, os vetores são ordenados utilizando pseudo-ângulo em quadrado unitário.

Determinar o fecho convexo de um conjunto de n pontos do plano requer, na verdade, no pior caso, Ω(n log n) passos.

Algoritmos: 

 

1. "Força bruta"

Seja (p, q) todos os pares de pontos pertencentes ao conjunto C. Qualquer par que tenha todos os demais pontos de um único lado em relação à aresta, trata-se de uma aresta válida para o fecho convexo.

 

Complexidade: O(n³)

 

2. Jarvis
3. Graham
4. Dividir-para-conquistar:
   4.1. Quickhull (em analogia com Quicksort)
   4.2. Mergehull (em analogia com Mergesort)

Os algoritmos de Jarvis e Graham serão melhor explorados nas futuras postagens.